Master Thesis Prize 2023 – Honorable mention
The Talbot effect, named after Henry Fox Talbot for its original discovery in 1836, is a lensless self-imaging phenomenon which describes revivals of periodic field patterns upon evolution of the field. More specifically, the self-imaging occurs upon a quadratic phase modulation in the Fourier dual domain of the periodic structure. Perhaps the most well-known example of the effect is the self-imaging of light transmitted through a grating, where the optical field reconstructs the grating structure at a specific propagation distance known as the Talbot length . In this case, the free-space propagation induces quadratic phase modulation in momentum space (under the paraxial approximation), mediating the self-imaging process of the spatially periodic grating structure. Besides the full (integer) self-images of the initial field at integer multiples of the Talbot length ZT, at fractions p/q ZT with coprime p and q, so called ‘fractional’ revivals occur: At these distances, the initial periodic field pattern is similarly reconstructed, but in this case with a 1/q fraction of the original periodicity (See Fig. 1b). With this, one can control the field periodicity just by propagation of different fractions of the Talbot length.
The Talbot effect is ubiquitous across all types of waves. It has been observed in a multitude of different Fourier-connected degrees of freedom, e.g. space-momentum, time-frequency, etc., and different types of waves, such as optical waves, water waves, electrons, atoms, even large molecules. Here, we focus on the azimuthal self-imaging of optical waves (aka the cylindrical Talbot effect) in step-index multimode fibers. A schematic representation of the effect is shown in Figure 1a. In Figure 1b there is a 2D simulation of the field evolution associated with the azimuthal Talbot effect, known and named for its distinctive looks as the Talbot carpet. The insets on the top show the transverse field distributions in the azimuthal angle – one can imagine connecting the top and bottom of the Talbot carpet to form a cylinder! This geometry is special in the sense that the periodicity of the azimuthal coordinate itself lifts the requirement for a periodic field – or in other words, any field is azimuthally periodic with a period of 2π radians.
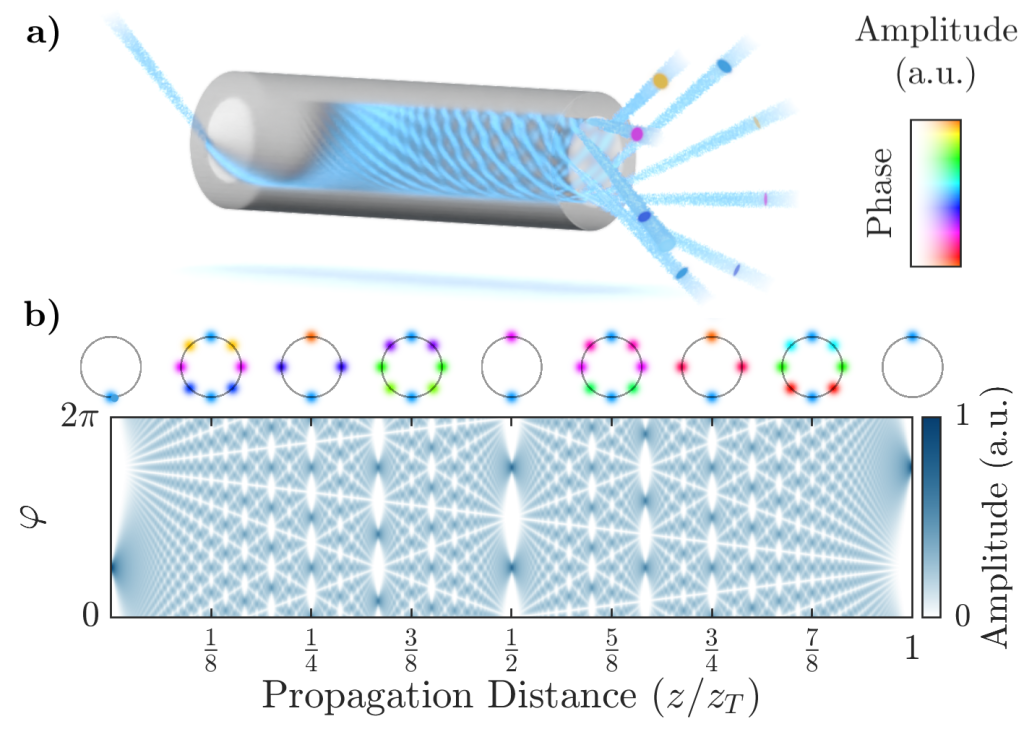
Figure 1: a) Schematic representation of the azimuthal Talbot effect in a step-index multimode fiber, showcasing an 8-fold fractional self-imaging of the input field. b) 2D simulation of the azimuthal Talbot effect, and the associated Talbot carpet.
The Fourier dual space of the azimuthal angle is known as the orbital angular momentum (OAM) space, a discrete space of eigenmodes of the OAM operator, i.e., light beams with helical wavefronts. The helicity of the wavefront is defined through the OAM topological charge l, corresponding to l rotations of the wavefront around the optical axis in one wavelength, or equivalently, a 2πl phase gradient around the azimuth in the transverse spatial field distribution of the beam.
The self-imaging effect in the azimuthal angle relies on the quadratic phase modulation of these OAM modes. This was previously shown to naturally occur through modal dispersion in ring-core fibers, i.e., specialty optical fibers where the light is transversely confined in a ring structure. In fact, I stumbled upon the topic of my thesis on accident while working with the self-imaging effect in these ring-core fibers: Due to a misalignment, the laser beam incident on the ring-core fiber was focused at an angle near the cladding-air interface of the fiber. To my surprise, nine equidistant spots around the azimuth appeared at the output facet of the fiber, resembling a 9-fold self-image of the input beam! This initiated the hypothesis that the set of cladding modes (similar to step-index fiber modes) excited by the misaligned laser must also support the self-imaging effect.
Luckily enough the hypothesis turned out to be correct. The azimuthal Talbot effect is indeed supported by specific modes of step-index multimode fibers known as whispering gallery modes (WGM), named after the analogous acoustic modes behind the famous acoustic whispering galleries. In the ray picture, one can imagine light rays circling the core near the core-cladding interface, with continuous total internal reflection bounding the light in the core region. These WGMs follow an approximately quadratic dispersion with respect to the OAM topological charge l, mediating the Talbot self-imaging effect. See Figure 2 for a few examples of these WGMs. A laser beam focused near the cladding-air interface with an azimuthal incidence angle will excite a wide OAM spectrum of these modes, which will interfere upon propagation generating Talbot self-images of the incident beam.
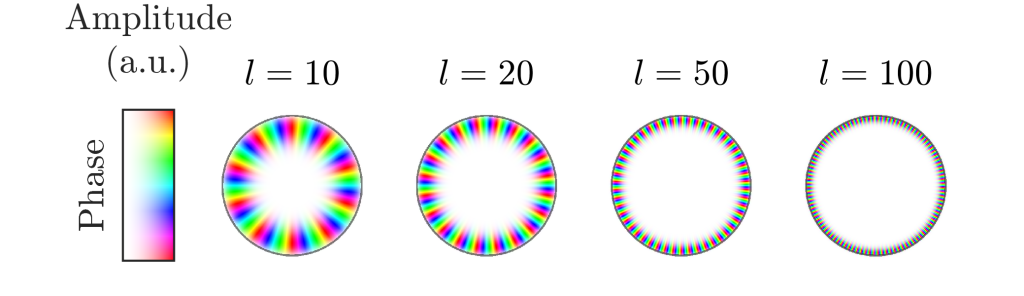
Figure 2: Transverse fields of whispering gallery modes (WGM) of a step-index multimode fiber with a core radius of 52.5 μm.
With this, it is time for an experiment. Using two different multimode fiber pieces with core radii 52.5 μm and 100 μm cut to lengths of 1/9 ZT and 1/30 ZT respectively, we set on to generate 9-and 30-fold fractional self-images of our input laser beam. Focusing an input laser beam near the core-cladding interface with a small azimuthal incidence angle, after careful alignment the WGMs of the fibers are excited and interfere together to form Talbot self-images. In Figure 3, experimentally realized fractional Talbot self-images of the input laser beam are seen, imaged at the output facets of the two fibers.
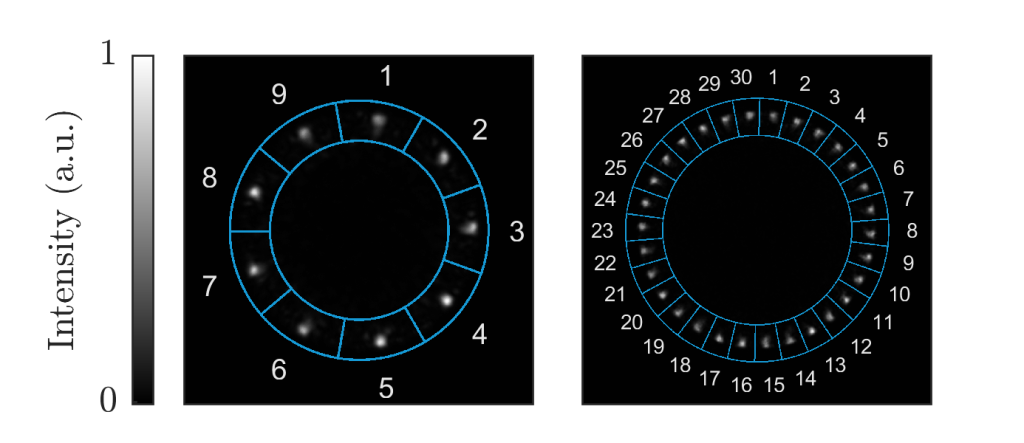
Figure 3: 9- and 30-fold fractional Talbot self-images of an input laser beam with whispering gallery modes of step-index multimode fibers. The input intensity distribution would correspond to just one of these spots incident on the fiber.
So, it works, but what is it all good for? Well, the fractional self-imaging process can be though of as a coherent, (arbitrarily) high-order beam-splitting operation. In fact, a device capable of N-fold fractional self-imaging is directly an N-to-N coupler, or a beam splitter with N input and output ports, which are ubiquitous in photonics, e.g. in classical and quantum photonic information processing protocols, multipath interferometry and optical multiplexing. Our beam splitters are further quite power efficient and yield uniform output power distributions, nearing state-of-the-art even with all imperfections of our basic experimental setting.