The Finnish Physical Society awards an annual prize for the excellent Master’s thesis in the field of physical sciences. The purpose of this prize is to support early career researchers and acknowledge them for the exceptional work. The winner(s) are selected by the board based on the thesis work, references and articles/videos made by the finalists.

Eric Hyyppä (Aalto University) received the shared second prize in Young Physicist 2020 competition. Below is the article he wrote about his thesis work.
In recent years, the research on quantum computing has witnessed a surge of interest evoked by the potential of this emerging technology and the experimental observation of quantum supremacy by Google’s quantum team in 2019. In Finland, significant research efforts are also under way to build a Finnish quantum computer in a collaboration project between VTT and IQM Quantum Computers. The interest towards quantum computing stems from the fact that an ideal quantum computer could, in theory, provide vast speed-ups in certain computational problems. In contrast to classical computers, quantum computers utilize two-level quantum systems, i.e., qubits to perform computations, and the potential speed-ups are based on a clever exploitation of superposition, entanglement, and interference of probability amplitudes in multi-qubit quantum processors. For example, a large-scale quantum computer could factorize large integers in a reasonable amount of time, speed up the search of unstructured databases, or simulate quantum-mechanical systems, such as intermediate-sized molecules, with possibly exponential time and memory savings. However, many of the potential applications of quantum computers will require fault tolerance enabled by quantum error correction, the realization of which remains challenging.
Currently, superconducting circuits are regarded as one of the leading candidates for building a large-scale fault-tolerant quantum computer. Namely, superconducting circuits satisfy the five DiVincenzo’s criteria required from a physical quantum-computing system:
- Superconducting circuits can be used to implement qubits that can be fabricated in a scalable fashion,
- Superconducting qubits can be accurately initialized to a known quantum state before a quantum computation,
- Superconducting qubits exhibit long lifetimes in comparison with the duration of quantum gates used for the computation,
- Superconducting qubits can be used to realize a universal set of quantum gates, the control of which is carried out using microwave pulses and external magnetic fields, and
- The states of individual superconducting qubits can be measured with a good accuracy at the end of the computation.
In the superconducting-quantum-computing architecture, qubits are represented by low-loss anharmonic oscillators containing one or multiple Josephson junctions. Josephson junctions are circuit elements consisting of two superconducting electrodes separated by an insulating barrier, and they can be modelled with a lumped element circuit incorporating a non-linear inductor shunted by a capacitor. The quantum-mechanical energy spectra of superconducting circuits consist of infinitely many energy levels in contrast to ideal qubits that only have two energy levels. Importantly, the two lowest-energy states of a superconducting circuit can be used to implement a qubit provided that the energy separation between the ground state and the excited state of the circuit is sufficiently different from the other transition energies. Josephson junctions provide the non-linearity required for making this two-level approximation. To observe quantum effects, superconducting qubits need to be cooled to temperatures of approximately ten millikelvin with the help of dilution refrigerators.
Two important figures of merit for individual superconducting qubits are anharmonicity and coherence time. Anharmonicity measures the validity of the two-level approximation and it is defined as the difference of transition energies from the first excited state to the second excited state, and from the ground state to the first excited state. A high anharmonicity enables the implementation of fast quantum gates that lead to minimal leakage errors into states above the first excited state. In the commonly used transmon qubits, the anharmonicity is relatively low, which limits the speed of the quantum gates. The coherence time describes how long it takes for the qubit to lose its quantum information to the environment. The coherence of superconducting qubits is often degraded by noise due to charge and magnetic-field fluctuations in the environment of the qubit. In general, a large ratio between the coherence time and the duration of quantum gates is desirable, since this determines the upper bound for the number of quantum gates that can be used in a quantum computation.
In my master’s thesis, I propose and study theoretically a novel superconducting qubit circuit that may exhibit both a high anharmonicity and a high coherence. As illustrated schematically in Figure 1(a), the studied superconducting circuit consists of a grounded superconducting coplanar waveguide (CPW) resonator with a Josephson junction embedded in the center conductor of the resonator. If the circuit did not contain the embedded Josephson junction, the distributed CPW resonator would support harmonic normal modes corresponding to standing voltage waves. Importantly, the non-linear current-voltage characteristics of the embedded Josephson junction turn some of the normal modes into anharmonic oscillators, one of which can be used to implement a qubit. The frequency and anharmonicity of the modes can be controlled by applying an external magnetic field through the two superconducting loops of the circuit as illustrated in Figure 1(b). The external magnetic field namely induces a supercurrent across the center conductor of the resonator, which biases the Josephson junction and changes the value of the effective non-linear inductance of the junction.
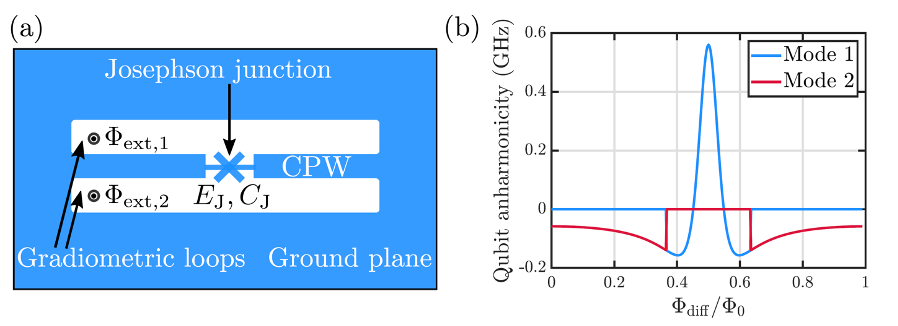
In my thesis, I derive the quantum-mechanical Hamiltonian of the proposed qubit circuit from first principles and find that the anharmonicity of the lowest-frequency mode can be 2-3 times higher than that of the commonly used transmon qubits for experimentally feasible parameter values at an appropriately chosen external magnetic flux. The relatively high value of anharmonicity is based on the negative effective inductance of the biased Josephson junction that leads to a partial cancellation of quadratic potential energy terms in the Hamiltonian of the circuit. The cancellation of quadratic potential energy terms ensures that the relative significance of higher order potential energy terms is increased, which enhances the anharmonicity.
In addition to a high anharmonicity, the studied circuit is also expected to exhibit a long coherence time. Firstly, the CPW resonator shunts the Josephson junction inductively, which should make the circuit immune to low-frequency charge fluctuations occurring in the environment of the qubit. Secondly, the two superconducting loops of the circuit are gradiometric meaning that the qubit is only sensitive to the difference of the external magnetic fluxes through the two loops, which provides protection against magnetic-field fluctuations. Thirdly, the maximum value of the anharmonicity is achieved at a so-called flux-insensitive sweet spot, where the frequency of the qubit does not change as a function of the external magnetic field to the first order. This provides further protection against magnetic-field fluctuations.
In conclusion, the studied superconducting circuit may provide a new type of a superconducting qubit that exhibits both a relatively high anharmonicity and coherence. Thus, it may be possible to implement faster quantum gates with the proposed qubit than with the conventional transmon qubits without sacrificing the fidelity of quantum logic operations. Exciting times are ahead since we plan to experimentally realize the qubit circuit. Then, we will see whether the promising theoretical qualities of the qubit are also seen in practice as suggested in our patent application.