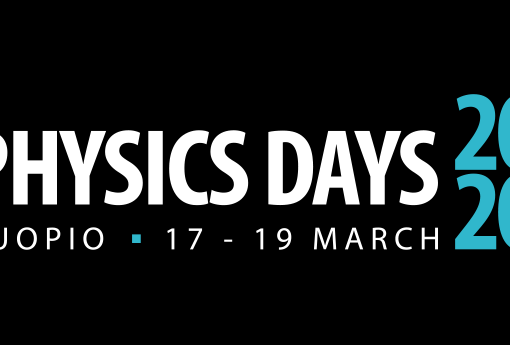The missing mass problem arose in the 20th century when observations of the dynamics of astrophysical objects could not be explained by ordinary luminous matter. This suggested the existence of some non-luminous excess mass, plentiful in the observable universe. Inspired by the non-luminous nature of this strange new substance, the term “dark matter” was coined, with little understanding of its true nature. Dark matter constitutes roughly a quarter of the energy budget of the universe, whereas visible matter adds up to less than five percent. A common hypothesis is that dark matter is a new particle that is not described by the Standard Model of particle physics.
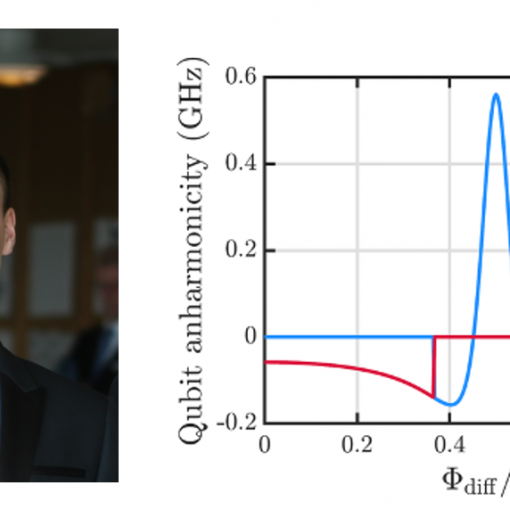
The Standard Model of particle physics is a quantum field theory that identifies and describes the elementary particles of ordinary matter, as well as tells us how the particles propagate in spacetime and interact with each other. The particle content of the Standard Model can be divided into two fundamental particle types, bosons and fermions (see fig. 1). Fermions are particles of half-integer spin and bosons are particles of integer spin (in units of the reduced Planck constant). What we understand as matter is constituted by spin-1/2 fermions. Electroweak and strong interactions are mediated by spin-1 bosons and the lone spin-0 scalar boson, called the Higgs particle, gives mass to all particles through a process called the Higgs mechanism.
Even though the Standard Model has been extremely successful in predicting and explaining the particle content and interactions observed in ordinary matter, there are phenomena it does not explain. The problem of interest in this master’s thesis is that of the missing mass, and cold dark matter is explored as a solution. The term cold refers to the non-relativistic nature of the dark matter candidate during the period of structure formation of the universe. The issue with naive cold dark matter models is that they are heavily constrained by direct detection experiments. For this reason, it is worthwhile to explore models, where dark matter is hidden in an extended sector of the Standard Model, and only able to interact with ordinary matter through a portal particle.
In my master’s thesis I examine an extension of the Standard Model with a new gauge boson — the vector dark matter candidate — and an SU(2) symmetric complex scalar field that interacts with the vector dark matter particle as well as the Standard Model Higgs particle. The new portal dark scalar field experiences mass mixing with the Standard Model Higgs, leaving the two propagating scalar mass eigenstates as superpositions of the dark scalar field and the Higgs field. One of these is then identified as the observed Higgs particle with a mass of 125 GeV. The aim of my thesis was to map out and constrain the parameter space of this hidden dark sector.
I found the model to have four free parameters, which can be chosen as the mass mixing parameter, the mass of the new propagating scalar field, the dark sector gauge coupling and the mass of the vector dark matter candidate. This four dimensional parameter space turns out to be rather constrained by current experiments and observations. Constraints from collider experiments have an effect in the low mass range of the dark matter particle. The direct detection constraint, on the other hand, has an effect throughout the parameter space by limiting the value for the dark matter — nucleon cross section. However, the allowed mass range for the dark matter particle still spans roughly 100–200 GeV (see fig. 2). The location of this range, which is the part of the blue curve within the green area, depends on the values of the other free parameters. By increasing the mass of the new propagating scalar field, the allowed range (the blue curve overlapping the green area) moves towards higher energies. The value of the mass mixing parameter alters the blue curve of the correct relic density vertically by deepening the dip to the viable region of the parameter space.
The viability of a dark sector with a vector dark matter candidate and an SU(2) scalar field manifests itself in a constrained parameter space that could still support the model. With the upcoming Laser Interferometer Space Antenna, the consequences of possible phenomena in the scalar sector of the model, such as phase transitions, could be examined. With the Large Hadron Collider, there is potential in the discovery of the new propagating scalar field through mass mixing with the Standard Model Higgs particle. Direct detection experiments provide a way of seeking the dark matter particle itself. With all these possibilities to shed light on the unresolved mystery of dark matter, the future may turn out extremely illuminating.