Master Thesis Prize 2023 – Winner
Gravitational waves are ripples in spacetime caused by accelerating masses, such as rotating neutron stars or black holes orbiting each other. Predicted by Einstein’s theory of general relativity, they were first observed in 2015 by the LIGO collaboration in the United States using a technique called laser interferometry. Gravitational waves change distances, but light speed remains constant. So we split a laser beam into two directions, let the resulting beams bounce off of mirrors positioned at equal distances from the laser source, and see if the lasers are still in phase when they return. If not, chances are that we just had a gravitational wave change the lengths of our two laser arms. The gravitational waves that passed through LIGO in 2015 came from a collision of two black holes.

Figure 1: Artist’s illustration of how gravitational waves from a single source might look like if we could observe them by eye. In the foreground, the Laser Interferometer Space Antenna. (Image: S. Barke / University of Florida)
Since then, this technique has allowed us to observe dozens of similar events. In addition to these astrophysical signals, gravitational waves are opening up a new window into the early universe. Our current horizon for cosmological observations lies at 380,000 years after the Big Bang, from where we now observe the first light as the Cosmic Microwave Background. Gravitational waves, on the other hand, have been traveling freely since the beginning of time, and could convey valuable information on events taking place in these early times.
One such event is a first-order phase transition as the universe cools down. In this process, bubbles of the new phase grow and eventually collide, which could generate gravitational waves observable at the millihertz frequencies today. There are many competing phase transition models, each of which give rise to gravitational waves with different frequencies and amplitudes. All of these, however, are so low in frequency that our current ground-based interferometers cannot detect them.
They could instead be observed by LISA, the Laser Interferometer Space Antenna. LISA is a spaceborne gravitational wave mission led by the European Space Agency, set to be launched in the mid-2030s. LISA consists of three satellites orbiting the Sun in a triangular formation, with laser beams traveling between each satellite. The laser arm length of LISA is 2.5 million kilometers, which makes it sensitive to millihertz frequencies. That is exactly where the potential phase transitions await.
Laser interferometry with free-falling satellites is somewhat more challenging than with static instruments on Earth. For example, there are time delays that come into play due to the inevitable shifting of the relative positions of the satellites. And although we are free of Earth’s noises, there are still various noise sources that must be recognized and modeled
beforehand. These include instrument noises, as well as gravitational wave signals we may perceive as noise. One such signal we are especially worried about here is the foreground from millions of white dwarf binaries in our galaxy, which also peaks in the millihertz range.
Unlike ground-based instruments, we cannot afford to test and upgrade LISA in its working environment. For that reason, the LISA Consortium have developed the LISA Simulation Suite, a tool that mimics the functionality of the instrument as closely as possible. For my thesis, I used the Simulation Suite to create 25 different datasets. Each of them contained a
different phase transition model, as well as instrument noises and a galactic binary foreground. The aim was to see how well LISA would be able to detect different phase transition models despite the unfortunate overlap with the galactic foreground.
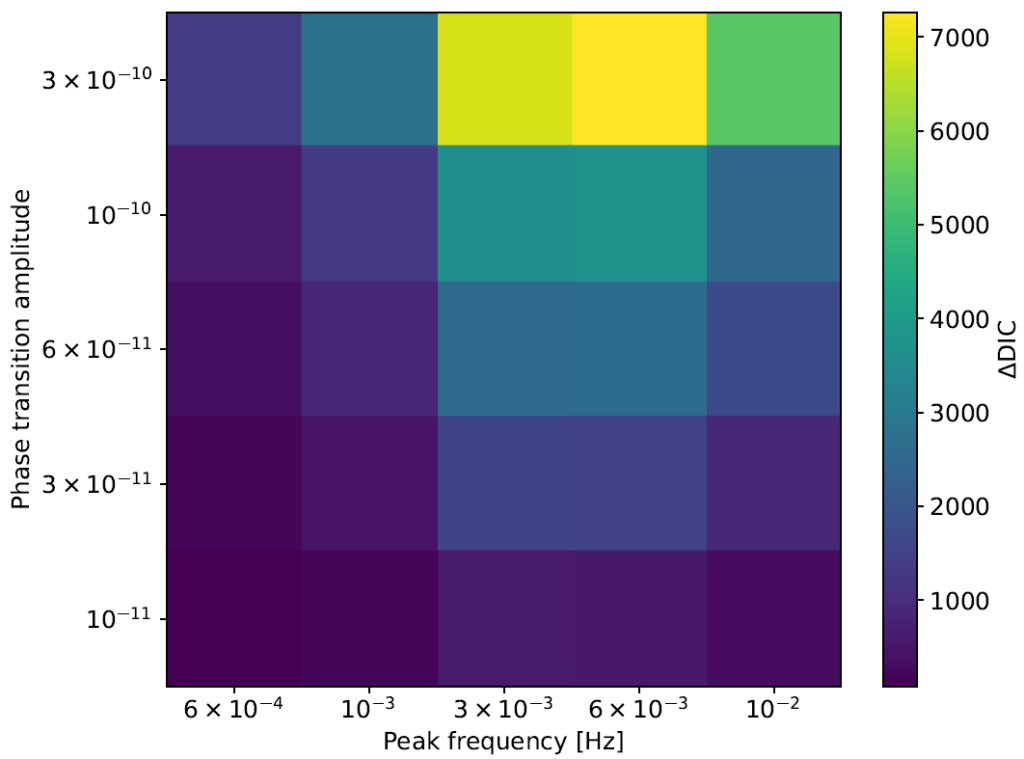
Figure 2: Map of the detectability of 25 phase transition models with different amplitudes and frequencies. A brighter square signifies a stronger detection.
I carried out statistical analyses to recover the underlying phase transition signal for each of the 25 cases. Figure 2 shows the detectability of the phase transition in each case, as assessed by the Deviance Information Criterion. The results point towards a higher detectability for signals with higher amplitudes, which is expected. We also get better detectability for signals in the millihertz range, where LISA is expected to reach its peak sensitivity. This suggests that the galactic foreground is less of a distraction to our observations than the instrument noises, which set limits in the upper and lower extremes of the frequency range of LISA.




