Kaapo Seppänen, University of Helsinki

Quantitatively understanding the thermodynamic properties of dense strongly interacting matter has recently become a hot topic in nuclear and particle physics. The leading factors behind this are major observational advances in neutron star physics, including the famous observation of gravitational waves from neutron star mergers by the LIGO and Virgo observatories and the more recent simultaneous mass–radius measurements by the NICER experiment. The data emerging from these sources can be translated to information about the equation of state of dense strongly interacting neutron-star matter. However, to make definitive statements about the nature of matter in these extreme conditions, one also needs complementary theoretical insights from the particle physics side.
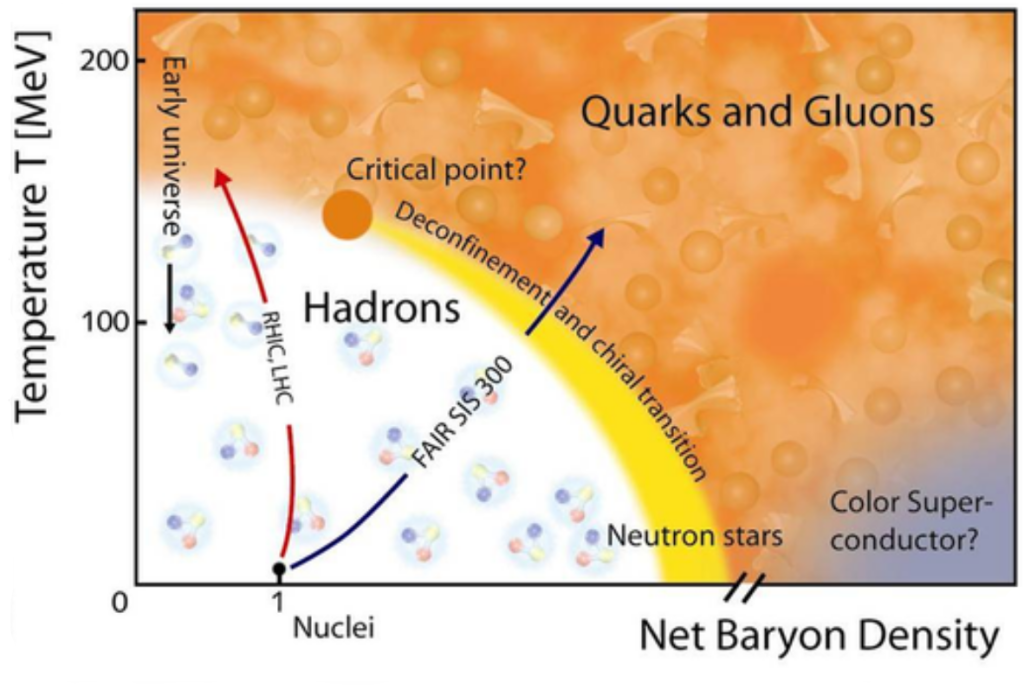
Quantum Chromodynamics (QCD) is the established quantum field theory describing the strong nuclear interaction, one of the four fundamental forces of Nature. QCD describes how quarks and gluons, the elementary constituents of ordinary baryonic matter, interact together to form protons and neutrons, which in turn form atomic nuclei. The most fundamental entity describing the thermodynamic properties of QCD is its phase diagram, which incorporates multiple very nontrivial features (see Fig. 1). At low temperatures and densities, quarks and gluons are confined inside hadrons, but as the temperature or baryon density increases, the system undergoes a so-called deconfinement transition becoming a liquid of almost freely propagating elementary particles. In the region of high temperature and low density, where QCD matter is in quark–gluon-plasma phase, the thermodynamics has been thoroughly probed with nonperturbative lattice simulations. Unfortunately, the lattice approach cannot be applied to high densities due to the infamous Sign Problem, rendering our understanding of the dense regime of the phase diagram, and hence the character of neutron-star matter, incomplete.
At very high densities, safely on the deconfined side, the QCD phase diagram can be probed by a method referred to as perturbative QCD (pQCD). Due to asymptotic freedom, the QCD coupling constant g, describing the strength of the interaction, becomes small at high energy densities, implying that various physical quantities can be expanded as generalized power series in g. The coefficients of these perturbative series are then calculated order by order in g. At the moment, pQCD serves as the only first-principles method to produce quantitative and reliable predictions for high-density nuclear matter, making pQCD computations vital for understanding the extreme physics of neutron-star cores. On the downside, the approximative nature of pQCD requires the coupling g to take values smaller than those realized at the densities present inside physical neutron stars. In order to apply pQCD to moderate densities, the perturbative series have to be determined to very high orders, making practical calculations immensely challenging.
There is another practical challenge in modeling dense nuclear matter with perturbation theory. At high densities and/or temperatures quarks and gluons develop collective long-range interactions among themselves, analogous to charge screening effects in classical electrodynamics. In perturbative calculations, these effects manifest in infrared (long-wavelength) divergent physical quantities, which clearly signal the breakdown of the theory. Fortunately, by rearranging the perturbation series in a certain way, one can get rid of the infrared divergences and restore the predicting power of the theory. Braaten and Pisarski (1990) showed that this is accomplished by resumming an infinite number of infrared divergent Feynman diagrams containing so-called hard thermal loops (HTLs). Specifically, HTLs are the dominating parts of one-loop Feynman diagrams at long distances.
Making actual predictions within the HTL theory relies on explicit calculation of so-called self-energies in the HTL limit. Self-energy describes the energy that a particle has due to its interactions with the surrounding plasma, and the HTL limit provides the leading thermal contribution to the quantity. In my thesis, I have calculated the basic building blocks of the HTL resummation, the one-loop quark and gluon HTL self-energies. These leading-order self-energies have been used widely in the literature, but recently many high-order perturbative computations have reached a point where one has to extend the HTLs to the next-to-leading order (NLO). For instance, calculating the equation of state of dense nuclear matter at a new perturbative order to gain more accurate insight into neutron-star cores requires the two-loop gluon self-energy in the HTL limit at finite density.

To pave the road towards the gluonic two-loop self-energy computation, I have calculated the slightly simpler counterpart for the photon from quantum electrodynamics (QED) at finite density and temperature. In contrast to the gluon, the photon lacks self-interactions making the evaluation of its self-energy more tractable than that of the gluon. Even so, the computation turned out to be very nontrivial with numerous subtleties, and further serves as the first two-loop HTL self-energy calculation that accounts for finite density effects.
The motivation for obtaining the result is twofold. First, it may be directly applied to physical settings where a long wavelength photon propagates in a high-density and/or -temperature medium formed by quarks and gluons. Second, having gone through the jungle of calculations with photons has prepared me for extending the result to involve gluons. In principle this should be straightforward given the powerful tools of real-time formalism of thermal field theory that I have reviewed in detail and applied in my thesis. However, the intricacies arising from the self-interacting gluons should not be underestimated.
The two-loop HTL self-energy results from my thesis will be employed in the computation of the cold and dense equation of state of QED at the next-to-next-to-next-to-leading order providing an update to an over 40-year-old result. Importantly, the QED computation serves as a useful testbed for completing the previously mentioned analogous computation for dense nuclear matter. Those future results are expected to supply invaluable information on the nature of matter inside neutron-star cores and help us sharpen our understanding of the fascinating physics contained therein.