Toni Mäkelä, Aalto University
The Finnish Physical Society awards an annual prize for the excellent Master’s thesis in the field of physical sciences. The purpose of this prize is to support young researchers and acknowledge them for the exceptional work. The winner(s) are selected by the board based on the thesis work, references and articles/videos made by the finalists.
Toni Mäkelä was among the top four finalists and received honorary mention in Young Physicist 2019 competition. Below is the article he wrote about his thesis work.
In the Standard Model of particle physics, particles obtain their masses via the Higgs mechanism. The heaviest elementary particle in the model and observed in nature is the top quark. It has turned out heavy enough to affect the Higgs potential itself via higher-order corrections in perturbative quantum field theory [1]. If the relation of the theory and measurements is interpreted correctly and if there is no new physics beyond the Planck scale, our Universe appears to be metastable: between stable and unstable. However, a crucial question for such discussion is if the measured values are robust – a point addressed by the work discussed herein.
The top was first observed in 1995 by the DØ (D Zero) and the CDF collaborations at Fermilab’s Tevatron collider, which proceeded to measure its mass. This effort has since been joined by the ATLAS and CMS experiments of the LHC at CERN. Today, the top mass world average is 173.3 GeV, almost 1.4 times the mass of the Higgs boson. To make the units familiar, the proton mass is roughly 1 GeV. The top mass results from ATLAS, CDF and CMS agree within uncertainties. The average is lifted by the very precise DØ result lying about 2.5 GeV above the similarly accurate LHC measurements. This corresponds to almost 3 standard deviations.
Like most massive resonances produced in collider experiments, the top itself is never observed, only its decay products. The objects of interest to an experiment are jets, sprays of lighter particles stable enough to reach a detector volume within their lifetime. The reported accuracy of DØ comes from a very precise and unique jet energy calibration, a mapping between experimentally measured and theoretically simulated values. The magnitude of the calibration depends on the jet’s flavour, i.e. if it originated from a gluon, a heavy b-quark, or one of the light quarks u, d, s, c. Respectively, DØ had three different correction factors: Fgcorr, Fbcorr and Flqcorr. The top is too short-lived to form hadrons and jets of its own, but decays almost always into a W-boson and a b-quark, initiating a b-jet. This makes Fbcorr especially important for top studies. As a rule of thumb, the more Fbcorr is below unity, the larger the top mass is measured to be.
However, the various Fcorr factors presented by DØ in [2] appear very different between the second Tevatron run’s two epochs, dubbed IIA and IIB. In particular for b-jets, the Fbcorr used for IIB is significantly below that of IIA. As the amount of data collected during IIB far exceeds IIA, the DØ top mass result is dominated by analyses using the IIB corrections.
The DØ jet energy calibration method is based on the assumption that the relativistic four-momentum of a jet corresponds approximately to the four-vector sum of its constituent particles. First, the detector response to each individual particle is determined from a simulation where the detector is exposed only to particles of one type at a time. Determining suitable functional forms that fit this simulation yields a set of energy-dependent single-particle response (SPR) functions, also reported in [2].
The next step is to produce a Monte Carlo generated set of simulated events of producing a probe, a jet that is approximately back-to-back with a tag object. The tag must be an object that suffers a minimal energy loss in the detector and is easily identified in an experimental apparatus – for instance a very energetic photon. This is because a similar set of events must eventually be identified in detector data for comparison. The first step in accounting for detector effects is to reconstruct the simulated events by applying the SPR to all individual particles. The ratio of the reconstructed probe and tag transverse momenta, ergo the components perpendicular to the colliding beams’ axis, is computed as a function of an estimate for the jet’s energy. These ratios are then compared between the detector data and the reconstructed simulation. Since this reconstruction alone does not yet suffice to describe experimental data, additional fit parameters are introduced to the SPR used for hadrons, which are composite particles containing quarks and gluons. These parameters are subsequently tuned until simulation agrees with experiment.
The determination of the flavour-dependent correction factors begins by summing over the energies of all particles in a simulated jet such that each energy is multiplied by the previously tuned SPR of the corresponding particle type. This is divided by a similar sum, but using the original non-tuned SPR functions. The computation is performed for each jet, and the results are put into separate histograms for each jet flavour. Finally, the Fcorr are obtained by dividing these histograms by an all-flavour average and fitting a continuous function to the result. These functions are eventually utilized in any analysis relying on jet energy calibration, including measurements of the top mass.
The relevant analysis notes describing the DØ jet energy calibration were made public in 2018, allowing us to perform a first-ever reproduction of the method. We used independent Monte Carlo simulations to produce as similar samples as possible to those reportedly used by DØ in [2,3]. In any ambiguously explained steps, our choices were motivated by tracking down which option would best reproduce the DØ results at the various stages of the analysis chain when using the tuned SPR functions reported by DØ in [2] – going all the way from the tag and probe transverse momentum ratios to determining the final Fcorr correction factors.
After successfully reproducing the DØ method and their resulting Fcorr factors, we studied possible ways of improving the process. For instance, the SPR function tuning was modified to avoid unphysical behaviour in hadron responses. Furthermore, the final Fcorr were fitted using power laws with good extrapolation properties, whereas [2] suggest that the DØ fits incorporated at most second degree polynomials. With our procedure, the correction factors turned out very similar for both run IIA and IIB. This is illustrated in the figure, which compares our fits and DØ results for IIA and IIB2, the subepoch when most of run IIB data was collected and where the difference between DØ and our Fbcorr is the most crucial.
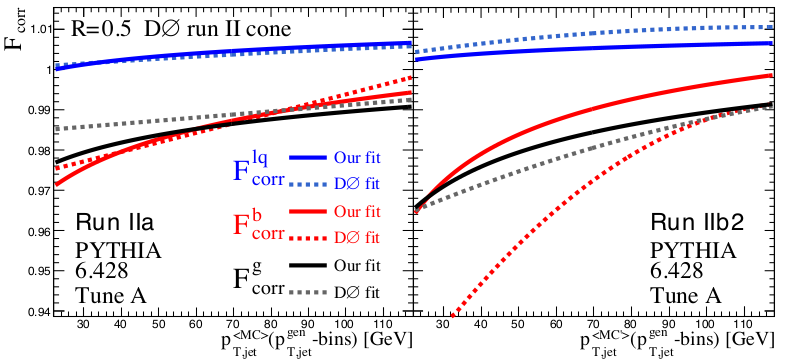
The studies serve as input to a publication examining the effect of the jet energy calibration on top mass measurements. Preliminary results indicate that this could be a possible explanation of the inconsistency between the top mass values obtained by DØ and the other collaborations ATLAS, CDF and CMS. In case a recomputation of the world average top mass is to follow, the interest will span both the experimental and theoretical communities in particle physics.
[1] A. Andreassen et al. “Scale Invariant Instantons and the Complete Lifetime of the Standard Model”. In: Phys. Rev. D97.5 (2018), p. 056006. [2] S. Atkins et al. “Correction For the MC-Data Difference in the Jet Response at DØ”. In: DØ note 6143 (2011); K. Augsten and Z. Ye. “Correction For the MC-Data Difference in the Jet Response at DØ for Run IIB”. In: DØ note 6368 (2013). [3] V. M. Abazov et al. “Jet energy scale determination in the DØ experiment”. In:Nucl. Instrum. Meth. A763 (2014), pp. 442–475.